做决定时，大脑中可能有这样的一个思考过程：

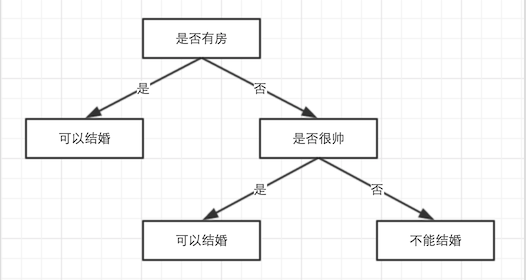
这样“精确”的逻辑可能是经历了很多事情才得到的。决策树也类似这个过程：

在样本上，通过精确地划分，形成这样树形的决策逻辑。

存在两种类型的节点：

• 内部节点：条件或者阈值，决定下一步应该去哪个子树
• 叶子节点：类型或者预测值

可以理解为：从上到下，通过内部节点将可能性空间不断细分，最终到达一个目标状态（叶子节点）。

基础知识

选择哪些维度以及如何划分是决策树的核心，也是最难的，需要一些知识准备。

信息熵

对一片文章的评价可能是信息量很大，也可能是废话连篇。那么：

能否量化信息的多少？

什么样的话是废话？

原来确定的事情，再说一遍就是废话，比如：太阳今天会从东边升起！

什么样的话信息量比较大？

原来不确定的事情，再说遍就比较确定了，比如：今天某个股票的财报很好，明天股票会大涨！

概率发生的变化越大（从无序到有序），信息量也就越大！而且信息量的多少应该满足：

• 非负
• 可加：f(xy)=f(x)+f(y)
• 连续
• 递减：概率越小，信息量越大

满足这些性质的函数只有：

$$
-log(x)
$$

而信息论祖师爷Shannon搞出来的信息熵的含义是：

系统中所含有的平均信息量的大小，或者是说，描述一个系统需要的最小空间。

于是，对于概率事件$(A_1,A_2,…,A_n)$，并且各事件对应的概率为$(p_1,p_2,…,p_n)$，则其信息熵为：

$$
H(X) = -\sum p_i \times log(p_i)
$$

熵函数图形如下：

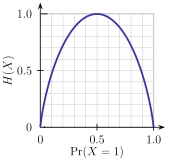
多维度的信息熵

当系统中有两个维度时，其联合熵为：

$$
H(X,Y) = \sum_i \sum_j - p(x_i, y_j) \times log(p(x_i, y_j))
$$

显然，当$X$、$Y$不相关时有：

$$
H(X,Y) = H(X) + H(Y)
$$

并且，当向系统中引入新的维度以后，信息熵总数增加的：

$$
H(X,Y) \geqslant H(X) \ \ \ \ H(X,Y) \geqslant H(Y)
$$

当某个维度（条件）的值固定（已知）时，其他维度的熵为条件熵：

$$
H(Y|X) = \sum p(x_i) \times H(Y|x_i) = H(X,Y) - H(X)
$$

两个维度相关的话，说明他们之间有公共的信息（互信息）：

$$
\begin{align}
I(X;Y) & = H(X) - H(X|Y) \\
& = H(Y) - H(Y|X) \\
& = H(X) + H(Y) - H(X,Y) \\
& = H(X,Y) - H(X|Y) - H(Y|X) \\
& = \sum \sum p(x,y) \times log \left ( \frac{p(x,y)}{p(x)\times p(y)}\right )
\end{align}
$$

信息增益和信息增益比

互信息从另外一个角度理解：

当某个维度固定之后，对其他维度的信息熵的影响多少。

此时的说法就是信息增益了。直观上信息增益越大越相关，但是缺点很明显：

不同维度的基数不一样，大家的起跑线也就不同了。

可以用通过影响量的比例（信息增益比）来衡量效果的好坏：

$$
I_r = \frac{I(X,Y)}{I(X)}
$$

基尼系数

劳伦茨曲线是由经济学家劳伦茨提出用来描述收入分配：

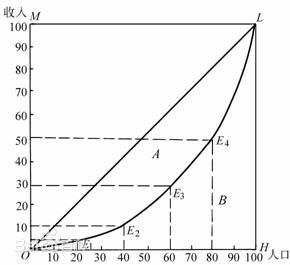
其中：

• 横轴为人口累计（人口对应的收入从低到高）
• 纵轴为收入累计

阿尔伯特·赫希曼在此基础上提出基尼系数，用来描述是否平均（面积的比例，比例越大越不平均）：

$$
Gini = \frac{A}{A+B}
$$

对一个数据集上的概率，$Gini$系数计算方式如下：

$$
Gini = 1 - \sum p_i^2 = \sum p_i \times (1-p_i)
$$

基尼系数越大系统越混乱（不确定），貌似和经济学中的概念不大一样，反而看$y=x \times (1-x)$的图形更好理解一些（先留个坑）：

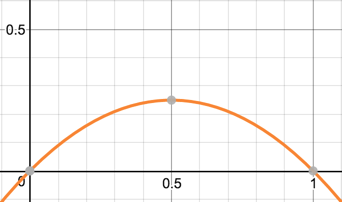
算法流程

不同决策树算法的流程是相似的：

• 生成树模型
• 剪枝
• 预测：回归/分类，也就是模型的使用

下面依次来看！

生成树

总体来说是希望在细分样本的过程中，不确定性不断地降低，不同衡量的准则产生了不同的算法。

ID3

衡量标准为信息增益：

每次选择出来的维度，信息增益越大越好。

举个栗子：