单纯形法 | wsztrush 

某公司生产玻璃产品，包括各种窗和玻璃门，该公司有三个工厂，分别负责：

1. 铝框架和硬件（每天4小时）
2. 木质框架（每天12小时）
3. 玻璃和组装（每天18小时）

高层决定将生产能力转移到有较大销售潜力的两种新产品：

1. 产品一每批需要工厂一1小时、工厂三3小时，每件利润3；
2. 产品二每批需要工厂二2小时、工厂三2小时，每件利润5；

高层现在很头疼，怎样安排生产才能使得利润最大？假设产品一生产$x_1$、产品二生产$x_2$，得到数学模型如下：

$$
\begin{aligned}
max\ Z &= 3x_1 + 5x_2 & \\
s.t.\ &x_1 & \leqslant & 4 \\
& 2x_2 & \leqslant & 12 \\
& 3x_1 + 2x_2 & \leqslant & 18 \\
& x_1 \geqslant 0, x_2 \geqslant 0 \\
\end{aligned}
$$

单纯形法就是要解决这种在有限制的情况下最优解！

统一模型及解法

图形总是更直观一些，将限制条件所代表的区域（可行域）画到图上：

而目标函数如下，并且可以上下移动，上移时收益会增大：

发现在(2,6)的时候会取到最大值36：

从图形上可以看到一些性质：

1. 约束条件围成了一个凸多边形；
2. 最优解一定会出现在某个顶点上；

对二维、简单的问题用图形来找答案是没有问题的，但是更高维度就不现实了，需要找到统一的形式和代数解法！

标准形式

在数学上常用的套路是：

1. 找到标准问题的各种解法；
2. 将其他形式的问题通过各种方法转换成标准问题；

这类最优化问题的标准形式用向量描述如下：

$$
\begin{aligned}
max\ Z& = CX \
s.t. & AX = b \
& X \geqslant 0
\end{aligned}
$$

其中：$C=\begin{bmatrix} c_1, …, c_n\end{bmatrix}$，$A=\begin{bmatrix} a_{11} & … & a_{1n}\ … & & … \ a_{m1} & … & a_{mn}\end{bmatrix}$，$b=\begin{bmatrix} b_1 \ … \ b_m\end{bmatrix}$，$X=\begin{bmatrix}x_1 \ …\ x_n\end{bmatrix}$，特点为：

1. 目标函数：最大化
2. 约束条件：等式
3. 决策变量：非负

当存在$c_i > 0$且对应的$x_i$，那尝试将$x_i$变大目标函数就会增大，单纯形法的求解过程就是不断地寻找最合适的$x_i$，在约束条件允许的条件下增大它：

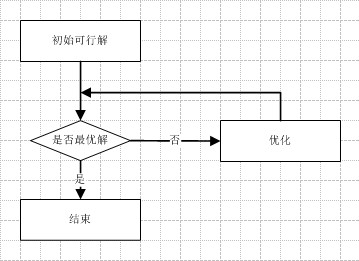
初始可行解

对原矩形分解得到（其中$B$可逆）：

$$
A=\begin{bmatrix}B,N\end{bmatrix}
$$

相应的$X$可以分解为：

$$
X=\begin{bmatrix}X_B \ X_N\end{bmatrix}
$$

其中$X_B$为基变量、$X_N$为非基变量，由约束得到：

$$
\begin{bmatrix}B,N\end{bmatrix} \begin{bmatrix}X_B \ X_N\end{bmatrix} = b \Rightarrow
BX_B + NX_N=b \Rightarrow
X_B = B^{-1}b-B^{-1}NX_N
$$

令$X_N=0$即得到了一个初始可行解。说起来容易做起来难，可逆总感觉是个比较麻烦的事情，有没有一些简单的办法？

大M法

在原有的矩阵中找可逆子阵毕竟还是困难的，那么另辟蹊径：

大M的思路不是去寻找，而是去构造。

设$M$是一个无穷大的数，对于：

$$
\begin{aligned}
max\ z =\ & x_1 + x_2 \
& x_1 + 2x_2= 10
\end{aligned}
$$

处理之后得到：

$$
\begin{aligned}
max\ z =\ & x_1 + x_2 - Mx_3 \
& x_1 + 2x_2 + x_3= 10
\end{aligned}
$$

由于$x_3$在目标函数的中的系数巨大无比，那么在有最优解时必然有$x_3=0$，而初始可行解显然可以为$\begin{bmatrix}x_3\end{bmatrix}$。

两阶段法

大M法虽好，但是计算机终究是不动无穷大的M为何物，为了求得可行解，可构造新问题（第一阶段）：

$$
\begin{aligned}
max\ z =\ & -x_3 \
& x_1 + 2x_2 + x_3= 10
\end{aligned}
$$

得到的结果不是0则说明原问题无解，否则以第一阶段的结果$\begin{bmatrix}10,0,0\end{bmatrix}$为初始可行解求原问题最优解（第二阶段）。

最优性校验

对于一个基本可行解$X=\begin{bmatrix}X_B \ X_N \end{bmatrix}$对应的目标值为：

$$
\begin{aligned}
Z & = CX \
& = \begin{bmatrix}C_B,C_N \end{bmatrix}\begin{bmatrix}X_B \ X_N \end{bmatrix} \
& = C_BX_B + C_NX_N \
& = C_B(B^{-1}b-B^{-1}NX_N)+C_NX_N \
& = C_BB^{-1}b+(C_N-C_BB^{-1}N)X_N \
& = C_BB^{-1}b + \sigma_NX_N
\end{aligned}
$$

如果存在$\sigma_i > 0$，那么我们只需要增大相应的$x_i$即可得到更大的Z，也就是说：

当前解为最优解等价于$\sigma_N \leqslant 0 $。

优化

当有多个$\sigma_i > 0$时，选择最大的一个来增加对应的$x_i$，有点像：

向最大的梯度增加。

最大的梯度并不一定意味着最大的增长量。每次优化都会涉及到两个动作：

1. $x_i$从0变大的过程，称为入基
2. 由于约束条件的存在，在$x_i$变大的时候必然有个$x_j$会减小到0，称为出基

再来看：

$$
X_B = B^{-1}b-B^{-1}NX_N \Rightarrow X_B = B^{-1}b-B^{-1}P_ix_i
$$

其中$P_i$为$x_i$对应的系数向量，于是，$X_B$中首先变成0的为：

$$
min\left { \frac{(B^{-1}b)_k}{(B^{-1}P_i)_k}, (B^{-1}P_i)_k > 0\right }
$$

同时可以得到：

不存在$(B^{-1}P_i)_k > 0$时，无最优解。

改进

在单纯形法的计算过程中，最大的工作量在于需要不停地求解$B^{-1}$，那么：

是否可以简化$B^{-1}$的计算？

假如当前的逆矩阵为$B^{-1}$，基为$B=\begin{pmatrix}P_1, P_2, …, P_l, …P_m \end{pmatrix}$，新基为$B_1=\begin{pmatrix}P_1, P_2, …, P_k, …P_m \end{pmatrix}$，对比：

$$
\begin{aligned}
B^{-1}B & = \begin{pmatrix} B^{-1}P_1,B^{-1}P_2,…,B^{-1}P_l,…,B^{-1}P_m\end{pmatrix} \
& = \begin{pmatrix} e_1,e_2,…,e_l,…,e_m\end{pmatrix} \
& = I \
B^{-1}B_1 & = \begin{pmatrix} B^{-1}P_1,B^{-1}P_2,…,B^{-1}P_k,…,B^{-1}P_m\end{pmatrix} \
& =\begin{pmatrix} e_1,e_2,…,B^{-1}P_k,…,e_m\end{pmatrix} \
\end{aligned}
$$

假设不同的列的值为：

$$
B^{-1}P_k = \begin{bmatrix} a_{1k} \ a_{2k} \ … \ a_{lk} \ … \ a_{mk} \end{bmatrix}
$$

于是有：

$$
E_{lk}= (B^{-1}B_1)^{-1} = \begin{bmatrix}
1 & 0 & & -\frac{a_{1k}}{a_{lk}} & & 0 \
0 & 1 & & -\frac{a_{2k}}{a_{lk}} & & 0 \
& & \ddots & \vdots & & \
& & & \frac{1}{a_{lk}} & & \
& & & \vdots & \ddots & \
0 & & & -\frac{a_{mk}}{a_{lk}} & & 1
\end{bmatrix}
$$

推导得到：

$$
E_{lk}= (B^{-1}B_1)^{-1} = B^{-1}_1B \Rightarrow B^{-1}_1 = E_{lk}B^{-1}
$$

例子

问题如下：

$$
\begin{aligned}
max \ Z = & 3x_1 + 2x_2 \
& x_1 + x_2 + x_3 = 40 \
& 2x_1 + x_2 + x_4 = 60
\end{aligned}
$$

解：
得到$C=(3,2,0,0)$，$A=\begin{bmatrix}1&1&1&0 \ 2&1&0&1\end{bmatrix}$，$b=\begin{bmatrix}40\60\end{bmatrix}$，容易看到基变量为$x_3,x_4$，非基变量为$x_1, x_2$：

$$
B_0 =(P_3, P_4)= \begin{bmatrix}1 & 0 \ 0 & 1 \end{bmatrix} = B_0^{-1} \
X_B = B_0^{-1}b = \begin{bmatrix} 40 \ 60 \end{bmatrix} \
X_0 = \begin{bmatrix} 0 \ 0 \ 40 \ 60 \end{bmatrix}
$$

最优性校验：

$$
\begin{aligned}
\sigma_N & = C_N-C_BB^{-1}_0N \
& = (c_1,c_2) - C_BB^{-1}_0(P_1, P_2) \
& = (3,2)-(0,0)\begin{bmatrix}1&0\0&1\end{bmatrix}\begin{bmatrix}1&1\2&1\end{bmatrix} \
& = (3,2) > 0
\end{aligned}
$$

得到$x_1$为入基，接着：

$$
\begin{aligned}
B_0^{-1}P_1 & = \begin{bmatrix}1&0\0&1\end{bmatrix}\begin{bmatrix}1\2\end{bmatrix} \
& =\begin{bmatrix}1\2\end{bmatrix} \
& > 0 \
min{\frac{(B_0^{-1}b)_3}{(B_0^{-1}P_1)_3},\frac{(B_0^{-1}b)_4}{(B_0^{-1}P_1)_4}} & = { \frac{40}{1},\frac{60}{2}} \
& = \frac{60}{2}
\end{aligned}
$$

得到换出变量应该为$x_4$。此时基变量为$x_3,x_1$，非基变量为$x_2,x_4$，更新逆矩阵为：

$$
B_1^{-1}
= E_{41}B_0^{-1}
=\begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}\begin{bmatrix}1&0\0&1\end{bmatrix}
=\begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}
$$

开始第二次迭代：

$$
X_B
=B_1^{-1}b
=\begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}\begin{bmatrix}40\60\end{bmatrix}
=\begin{bmatrix}10\30\end{bmatrix} \
X_1=\begin{bmatrix}30\0\10\0\end{bmatrix}
$$

最优性校验：

$$
\begin{aligned}
\sigma_N & = C_N-C_BB^{-1}_1N \
& = (c_2,c_4) - C_BB^{-1}_1(P_2, P_4) \
& = (2,0)-(0,3)\begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}\begin{bmatrix}1&0\1&1\end{bmatrix} \
& = (\frac{1}{2},-\frac{3}{2}) > 0
\end{aligned}
$$

得到$x_2$为入基，接着：

$$
\begin{aligned}
B_1^{-1}P_2 & = \begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}\begin{bmatrix}1\1\end{bmatrix} \
& =\begin{bmatrix}\frac{1}{2}\ \frac{1}{2}\end{bmatrix} \
& > 0 \
min{\frac{(B_1^{-1}b)_3}{(B_1^{-1}P_2)_3},\frac{(B_1^{-1}b)_1}{(B_1^{-1}P_2)_1}} & = { \frac{10}{1/2},\frac{30}{1/2}} \
& = \frac{10}{1/2}
\end{aligned}
$$

得到换出变量应该为$x_3$。此时基变量为$x_2,x_1$，非基变量为$x_3,x_4$，更新逆矩阵为：

$$
B_2^{-1}
= E_{32}B_1^{-1}
=\begin{bmatrix}2&0\ -1&1\end{bmatrix}\begin{bmatrix}1&-\frac{1}{2}\0&\frac{1}{2}\end{bmatrix}
=\begin{bmatrix}2&-1\ -1&1\end{bmatrix}
$$

开始第三次迭代：

$$
X_B
=B_2^{-1}b
=\begin{bmatrix}2&-1\ -1&1\end{bmatrix}\begin{bmatrix}40\60\end{bmatrix}
=\begin{bmatrix}20\20\end{bmatrix} \
X_2=\begin{bmatrix}20\20\0\0\end{bmatrix}
$$

最优性校验：

$$
\begin{aligned}
\sigma_N & = C_N-C_BB^{-1}_2N \
& = (c_3,c_4) - (c_2,c_1)B^{-1}_2(P_3, P_4) \
& = (0,0)-(2,3)\begin{bmatrix}2&-1\ -1&1\end{bmatrix}\begin{bmatrix}1&0\0&1\end{bmatrix} \
& = (-1,-1) < 0
\end{aligned}
$$

非基变量对应的校验数没有正数，于是得到最优解。

思考

$n$个变量对应的系数可以看做是$m$维空间中的$n$个变量，可以从中选择$m$个作为基：

非基变量可以用基变量表示，也就是非基变量的变化可以用基变量的变化来表示。

对于非基变量有$x_i > 0$则可以看做是空间中的一个平面上方的部分：

约束条件对应的可行域便是由这些非基变量表示的平面包成的凸多面体。

非基变量都为0时，一定是在多面体的一个顶点上，此时如何找相邻的更优秀的顶点呢？沿着边找比较形象，但不容易实现，而换基的操作可以理解为：

尝试沿着某个平面法向量的方向增长来找更优的顶点。

多面体还是那个多面体，只不过是空间在不停地变换，而解则始终是在基的方向上搜索，这样可操作性会强一些。